یادآوری تقلب انتخاباتی خرداد ۱۳۸۸

مقدمه: شاید ارائه این مطالعه آماری از انتخابات ریاست جمهوری خرداد ۱۳۸۸ هشت سال پس از آن وقایع فاجعه آمیز در ایران دیر هنگام بنظر آید. اما سه انگیزه مرا وادار به پرداختن به این موضوع کرده است:

یکم: هشت سال پس از ۲۲ خرداد ۱۳۸۸ هنوز سرکوب، زندان و حصر معترضین به تقلب انتخاباتی به عنوان »فتنه گر» ادامه دارد و
دوم: هر چند که جمهوری اسلامی تقریبا هرگز انتخابات آزاد و سالم که در خور سنجش با معیار‌های رایج جهانی باشد به خود ندیده است اما تا پیش از خرداد ۱۳۸۸ تنها یکی از مولفه‌های انتخاباتی یعنی شمارش کم و بیش واقعی آرا را تا حدودی رعایت می‌کرد. انتخابات ۸۸ نقطه عطفی بود به سوی بازگشت از این حداقل انتخاباتی که پیامدش عملا می‌تواند نفی وجودی انتخابات و تهی کردن آن از هرگونه معنائی یاشد. ملاحظات مذکور مرا بر آن داشت که با انتشار تحلیلی ریاضی-آماری از نتیجه انتخابات خرداد ۱۳۸۸، به سویه‌ای از آن بپردازم که تاکنون با ژرفای کافی به آن پرداخته نشده است.

سوم: با توجه به تمرکزی که رژیم بر نامزدی ابراهیم رئیسی دارد بعید نیست بار دیگر به تقلب گسترده روی آورد. باید با انتشار دوبارۀ این پژوهش که کسانی که ممکن است قصد تقلب داشته باشند، اخطار کرد که تقلب شان پنهان نمی‌ماند.

پس از اعلام نتیجه انتخابات ۱۳۸۸ که برای بسیاری از شهروندان ایران گمان تقلب و دستکاری را برانگیخته بود کارشناسان بسیاری از ایران و جهان به تحلیل این نتیجه‌ها دست یازیده‌اند که بخش در خور توجه‌ای از آن‌ها در ویکیپدیا منتشر شده است اینجا.

موضوع نوشته حاظر معطوف به وجود شمار زیادی صندوق‌های رای است که تعداد کل آرای آن‌ها ضریبی از ۱۰۰ بوده‌اند. این واقعیت جلب توجه دیگر کارشناسان را نیز کرده بود و با نگاهی گذرا آن را به مثابه وجود تقلب ارزیابی کرده بودند. اما آنچه که این تحلیل را از دیگر تحلیل‌ها که اشاره‌ای گذار به این یافته‌ها کرده‌اند، متمایز می‌کند این است که کوشش کرده ام به لحاظ آماری موضوع وجود چنین صندوق‌ها را ژرفتر ارزیابی کنم و دریابم که آیا نتایج اعلام شده رخدادی تصادفی ناشی از یک انتخابات سالم‌اند یا پیامد دستکاری‌ای هدفمند و تقلب.

در تحلیل پیش رو به چگونگی توزیع آرا میان کاندیدا‌ها نپرداخته ام زیرا چنانکه ثابت شود که مجموع شمار رای‌ها در صندوق‌ها تصادفی نیستند - و لاجرم واقعی نیستند- ضرورتی برای ارزیابی چگونگی پخش ارقام غیر واقعی میان کاندیدا‌ها وجود ندارد.

نگارنده بلافاصله پس از انتخابات ۱۳۸۸ با همراهی آقای مسعود آذری تحلیلی به زبان انگلیسی از نتایج انتخابات منتشر کردیم که با در نظر گرفتن سویه‌های گوناگون موثر در انتخابات نشان می‌داد که تقلبی گسترده رخداده است. اما در پی این بودم که در یابم آیا می‌توان بدون در نظر گرفتن ملاحظات سیاسی، شیوه سازماندهی، نحوه و گسترۀ اعمال نفوذ نهاد‌ها و دیگر عوامل اثرمند، صرفا با اکتفا به نتایج رسمی اعلام شده از سوی دولت جمهوری اسلامی، ادعای معترضین جنبش سبز را در باره تقلب در انتخابات راستی آزمایی کرد؟

پایه این تحلیل ارقامی است که وزارت کشور جمهوری اسلامی در وبسایت خود از استان‌های تهران، لرستان، یزد، آذربایجان شرقی، اصفهان،اردبیل و کرمانشاه منتشر کرده است. کوششی است مبتنی بر این اصل که با کمترین ملاحظات سیاسی در یابم که آیا این نتایج می‌توانند ناشی از انتخاباتی سالم و دستکاری نشده باشند.

تنها ملاحظه سیاسی که مورد توجه قرار گرفته است اظهارات سخنگوی وقت شورای نگهبان آقای کدخدائی است پیرامون اینکه هیچیک از حوضه‌های رای گیری، به جز دو مورد آنهم با تاخیر ۲۰ و ۴۰ دقیقه‌ای، دچار کمبود تعرفه نبوده‌اند.

نتیجه گیری پژوهش پیش روی این است که در انتخابات ریاست جمهوری ۱۳۸۸ به احتمال قریب به یقین تقلب گسترده در حد عدد سازی صورت گرفته است. در لرستان بیشترین اندازه عدد سازی عریان صورت گرفته است. به نظر می‌اید که در مجموع، آرا صندوق‌ها به نحوی در میان کاندیدا‌ها تقسیم شده‌اند که به نتیجه از پیش اعلام شده برسند.

این نوشته را به دو بخش I و II تقسیم کرده‌ام: بخش I در برگیرنده نتایج تحلیل به شیوه‌ای که برای عموم خواننده گان مفهوم باشد و بخش II را برای کسانی که علاقمند به جزئیات تئوریک آن باشند، تنظیم کرده ام.

شیوه پرداختن به موضوع

برای بررسی واقعی یا ساختگی بودن نتایج انتخابات ۱۳۸۸ مجموع آرای تک صندوق‌های اخذ رای را تحلیل کرده ام. اگر نتیجه این باشد که این مجموعه‌های آرا تصادفی نیستند و لاجرم دستکاری شده و ساختگی‌اند، پرداختن به جزئیات توزیع شان در میان نامزد‌ها - که معرف همگان است، معنی چندانی ندارد از این روی به توزیع آرا نپرداخته ام و تنها به کل آرای هر صندوق اکتفا کرده ام.

نگاهی به شمار کل آرایی که در هر صندوق رای گیری ریخته شده است نشانه‌هایی از غیرعادی بودن آشکار می‌کرد. شاخص ترین نشانه‌ها این بود که تعداد صندوق‌هایی که تعداد کل آرای مأخوذ ه صریبی از ۱۰۰ بود به طرز چشمگیری فراتر از انتظار بود.

این مشاهده مرا بران داشت که تکرار دو رقم دست راست یعنی یکان و دهگان تعداد کل آرای ریخته شده به همه تک صندوق‌های رای را برای استان‌های تهران، لرستان، اصفهان، یزد، آذربایجان، اردبیل و کرمانشاه تحلیل کنم و برای مقایسه با نتایج دو انتخابات ایالتی وین ۲۰۱۴ و ۲۰۱۵ و یکی در برلین که هریک بزرگترین شهر اتریش یا آلمان نیز هستند، بسنجم.

I. چکیده نتیجه: پیش از پرداختن به جزئیات تئوریک رهیافتی که انتخاب کرده ام و برای خواننده گانی که ممکن است پرداختن به این جزئیات خارج از حوصله شان باشد چکیده یافته‌هایم را در بخش I در دو جدول ۱ و ۲خلاصه کرده ام:

به دلیل آنچه در بخش II توضیح خواهم داد احتمال تکرار k بار دو رقم یکان و دهگان تعداد کل آرای هر صندوق رای را می‌توان به میانجی توزیع بینومیال binomial distribution محاسبه کرد. برای تسهیل، نمونه وار محتوای صندوق‌هائی مانند ۲۰۰، ۵۰۰، ۹۰۰، ۱۵۰۰... را که یکان و دهگان شان صفر است E00 و ۱۶۹، ۸۶۹، ۲۰۶۹، ۲۳۶۹... را که یکان اشان ۹ و دهگان اشان ۶ است E۶۹ می‌نامیم. احتمال تکرار k بار E00 یا E۶۹ یا هر دو رقم دیگر Emn (m و n هریک می‌توانند ارقامی میان ۰ تا ۹ باشند) را می‌توان از راه توزیع بینومیال محاسبه کرد.

در مورد انتخابات ۱۳۸۸ ایران آنچه که فورا جلب نظر می‌کند فراوانی تکرار پاره‌ای از Emn‌ها به ویژه فراوانی چشمگیر تکرار E00‌ها است. جدول ۱ نتایج محاسبه این احتمالات را بازتاب داده است.

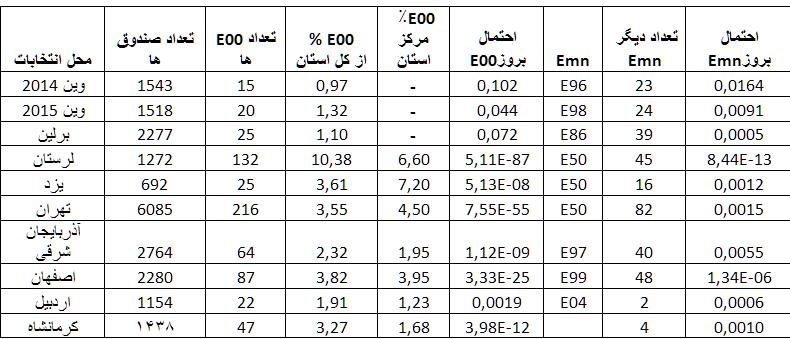
جدول۱: این جدول در برگیرنده ستون‌های «محل انتخابات»، «تعداد صندوق‌های» رای در انتخابات محل مربوطه، «تعداد E00‌ها» یعنی تعداد صندوق‌هائی که شمار کل رای‌های ریخته شده به آن‌ها ضریبی از ۱۰۰ باشد، «%E00 از کل استان» یعنی سهم در صد فراوانی صندوق‌های E00 از کل صندوق‌ها در استان مربوطه، «%E00 مرکز استان‌ها» یعنی سهم در صد صندوق‌های E00 از کل صندوقهای شهرهای مرکز استان، ستون «احتمال بروز E00» یعنی احتمال وقوع k بار تکرار E00 در استان‌ها، «Emn» دیگر شمار کل آرای اخذ شده در صندوق‌های رای با ارقام پایانی یکان و دهگان به ترتیب m و n است که فراوانی شان فراتر از حد انتظار بوده است، « تعداد Emn دیگر» شمار صندوق‌های که مجموع آرایشان به دو رقم mو n ختم می‌شوند و «احتمال بروزEmn » یعنی احتمال رخدادن این تعداد تکرار یک Emn معین مثلا اعدادی که به ۵۰ ختم می‌شوند.

از مشاهده جدول ۱ می‌توان به نتیجه گیری‌های زیر رسید:

۱. سه انتخابات در وین و برلین به مثابه نمونه انتخابات آزاد و سالم از یکسو و از دیگر سو هفت استان ایران مورد بررسی قرار گرفته‌اند. برای سه انتخابات نمونه درصد صندوق‌های E00 نسب به جمع کل تعداد همه صندوق‌ها میان ۰.۹۷٪ تا ۱.۳۲٪ قرار دارد که پیرامون اندازه مورد انتظار ۱٪ در نوسان است در حالیکه در استان‌های ایران میان ۱.۹۱٪ برای اردبیل تا ۳.۵۵٪ برای تهران تا ۱۰.۳۸٪ برای لرستان در تغییر است که از ۱٪ مورد انتظار بسیار فاصله دارد.

۲. برای همه موارد تکرار‌ها در جدول ۱ احتمال وقوع محاسبه شده‌اند. در حالیکه احتمال این تعداد تکرار‌ها ی رخداده برای وین و برلین میان ۰.۰۴، ۰.۰۷ و ۰.۱۰ است برای استان‌های ایران میان ۱۰-۸۷، ۱۰-۵۵، ۱۰-۲۵، ۱۰-۱۲، ۱۰-۹، ۱۰-۸ و ۰.۰۰۲، یعنی در سه مورد اول عملا احتمال وقوع صفر است و در بقیه موارد به استثنا اردبیل بسیار ناچیز. در مورد اردبیل نیز این احتمال وقوع E00، ۲۰ تا ۵۰ برابر کمتر از موارد وین و برلین است.

این ارقام نشان می‌دهند که نتایج اعلام شده از سوی وزارت کشور جمهوری اسلامی نمی‌توانند نتیجه یک انتخابات سالم و عاری از دستکاری باشند. در همینجا می‌توان دریافت که بالاترین اندازه تقلب در لرستان صورت گرفته است.

۳. پاره‌ای از مدعیان سالم بودن انتخابات بیان کرده‌اند که وجود بیش از انتظار صندوق‌های با شمار کل رای‌هائی که ضریبی از ۱۰۰(E00) هستند اینست که تعرفه‌های رای در دسته‌های صد تائی بسته بندی شده‌اند و مراکز اخذ رای دچار کمبود تعرفه شده باشند.

a. دو منطقه اخذ رای آن هم با تاخیر ۲۰ و ۴۰ دقیقه‌ای هیچ شعبه رای گیری در ایران دچار کمبود تعرفه نبوده است. عین گفته ایشان به نقل از وبسایت الف چنین است:
«مجموع تعرفه‌هايی که برای اين دوره از انتخابات چاپ شده بود، حدود ۶۰ ميليون برگه بود که شورای نگهبان در روزهای گذشته، برای اطمينان بيشتر، سه نفر از کارشناسان و بازرسان خود را به وزارت کشور فرستاد و آنها قراردادهای مربوط به چاپ، تعداد تعرفه‌هايی که در انبارها باقی مانده، تعداد تعرفه‌هايی که مصرف شده و تعداد تعرفه‌هايی که در صندوقها است را با آمار و ارقام و اسناد کافی جمعآوری کردند و گزارش آن را به اعضای شورای محترم نگهبان ارائه کردند و خوشبختانه هيچگونه مشکلی در اين زمينه نبوده و اين گزارش قابل ارائه است... روند رأیگيری، تنها در دو منطقه، آن هم به دليل استقبال گستردة مردم، با تأخير ۲۰ دقيقه و ۴۰ دقيقهای مواجه شد. غير از اين موارد هيچگونه گزارشی مبنی بر اينکه برگة تعرفه رأی در حوزهای وجود نداشته باشد به ما واصل نشده است»

b. نگاهی به توزیع صندوق‌های ضریب ۱۰۰ یا E00 نشان می‌دهد که در بیشتر استان‌ها در صد تعداد اینگونه صندوق‌ها در شهرهای مرکز بالاتر است تا در حاشیه‌های دور افتاده: استان تهران ۳.۵۵٪ در برابر شهر تهران ۴.۵۰٪، استان اصفهان ۳.۸۲٪ در برابر شهر اصفهان ۳.۹۵٪، استان یزد ۳.۶۱٪ در برابر شهر یزد ۷.۲٪. در موردی مانند استان لرستان که به شیوه‌ای مفرط یعنی تعداد E00 با ۱۰.۳۸٪ از انتظار بدور است، در مرکز ش خرم آباد هر چند که نسبت به حاشیه کمتر است اما با ۶.۶٪ یعنی ۶.۶ برابر ۱٪ مورد انتظار در صدی بسیار بالا است. در استان آذربایجان شرقی ۲.۳۲٪ در مقابل تبریز با ۱.۹۵٪ صندوق‌های E00 اختلافی بزرگ میان مرکز و حاشیه وجود ندارد. تنها در استان کرمانشاه در صد E00 دز شهر کرمانشاه با حاشیه اختلاف چشمگیر دارد (۱.۶۸٪ در برابر ۳.۲۸٪). در شهر مشهد، نیز سهم E00 از کل صندوق‌های شهر ۴.۳٪ است که احتمال رخدادنش با ۳.۲*۱۰-۱۳ بسیار ناچیز است- همین درصد برای آبادان ۳.۲٪ و برای اهواز ۲.۵٪ بوده است.

بنابراین اگر بیانات سخنگوی شورای نگهبان جدی تلقی شود نمی‌توان وجود وافر صندوق‌هائی با ضریب ۱۰۰ (E00) را با کمبود تعرفه توضیح داد: نخست اینکه تعرفه کافی در دسترس بوده است و دوم اینکه اگر کمبود جبران ناشدنی وجود می‌داشت قاعدتا می‌بایستی در حاشیه باشد نه در مراکز استان‌ها - که با واقعیت‌های مندرج در جدول ۱ مغایرت دارد.

وانگهی تعداد فراوان Emn، آنچنان که در جدول ۱ می‌توان مشاهده کرد، منحصر به E00 نیست بلکه E۵۰ (ضریبی از ۵۰)، E99، E45، E97 و E98 هم به حدی وافر پدیدار شده‌اند.

ضروری است خاطر نشان کنم که مثلا افزایش E00 از ۱٪ تعداد کل صندوق‌ها به ۲٪، احتمال را دو برابر کم نمی‌کند زیرا که چنین رابطه‌ای خطی نیست. مثلا برای اصفهان تغییر تعداد E00 از ۱٪ به ۲٪ احتمال وقوع آنرا تقریبا۱۴۰۰۰ بار کمتر می‌کند.

آزمون chisquare:
در مورد انتخابات ایران کوشش در این است که نشان دهم که ایا با حذف صندوق‌های ضریب ۱۰۰، E00، که به شدت از انتظار به دورند، رفتار دیگر داده‌ها در قیاس با انتخابات سالم وین و برلین چگونه است.

برای آزمودن اینکه ایا مجموعه‌ای از داده‌ها، مانند شمار آرای صندوق‌های اخذ رای، که باید خصلت تصادفی داشته باشند واقعاً به طور تصادفی بدست آمده‌اند یا مورد دستکاری قرار گرفته‌اند، روشی آماری وجود دارد که آنرا آزمون chi-square می‌نامند.

در جدول ۲ نتیجه کاربرد این آزمون بازتاب یافته است. لازم به تذکر است که چه در انتخابات سالم مانند وین و برلین و چه در انتخاباتی که ظن دستکاری و عدد سازی در آن‌ها وجود دارد مانند دیگر انتخابات مندرج در این جدول ۲، همه داده‌ها به درجات معینی تصادفی‌اند. یعنی حتی اگر اعداد ساختگی باشند باز هم روند ساختن شان تا حدودی تصادفی است. البته اعداد ساخته شده این قید را دارند که نتیجه تجمیع آن‌ها باید با نتیجه از پیش تعیین شده‌ای همپوش باشد. از اینروی قضاوت دقیق در پاره‌ای از موارد مشکل است اما می‌توان گرایش به سوی واقعی یا دستکاری بودن را نشان داد.

این آزمون بدو شیوه صورت گرفته است:
۱. سنجش همشکلی Uniformity : اگر انتخاباتی سالم باشد شمار آرا صندوق‌ها تصادفی‌اند. انتظار می‌رود که شمار تکرار‌ها k برای هر دو رقم دست راست معین Emn ۱۰۰/۱ تعداد کل صندوق‌ها N باشد. این تعداد تکرار N/۱۰۰ را اندازه منتظَر می‌نامند expected value. از سوی دیگر ارقامی در دست‌اند که شمار واقعی این تکرار‌ها Emn را نشان می‌دهند. این آزمون اندازه‌های واقعی را با اندازه‌های منتظَر می‌سنجد. در دو ستون جدول ۲ «آزمون chisq » و «آزمون chisq بدون تکرار‌های نا محتمل» احتمال‌هائی درج شده‌اند که می‌توانند نشان بدهند آیا اختلاف معنی داری میان اندازه واقعی و منتظَر وجود دارد. در آمار متداول است که چنانچه این احتمال بزرگتر از ۰.۰۵ باشد اختلاف معنی دار نیست یعنی تصادفی است و اگر کمتر از آن باشد اختلاف معنی دار است یعنی غیر تصادفی و می‌تواند نتیجه دستکاری باشد. این آزمون نشان می‌دهد که اگر همه داده‌ها را ملحوظ کنیم انتخابات وین و برلین کاملا خصلت تصادفی دارند در حالیکه هیچیک از ۷ انتخابات نامبرده ایران تصادفی نیستند. حال اگر موارد تکرار‌های بسیار نامتعارف مانند E00 را ملحوظ نکنیم باز هم نتایج لرستان، یزد، اصفهان و اردبیل غیر تصادفی‌اند یا به عبارت دیگر دستکاری شده‌اند.

۲. در سنجش با توزیع بینومیال و آزمون همپوشی با آن binomial fit
در این روش اندازه‌های واقعی تکرار‌ها با اندازه منتظَر از توزیع بینومیال سنجیده می‌شود. از آنجا که تعداد اندازه‌ها در این روش در قیاس با روش همشکلی کمتر است واکنش نتیجه محاسبه نسبت به تک داده‌هائی که خارج از انتظار هستند شدید تر است. ( در مورد نخست ۱۰۰ یا با حذف E00ها ۹۹ زوج از داده‌ها داریم در حالیکه در مورد دوم بسته به یزرگی استان شمار زوج‌های k واقعی و k منتظَر میان ۱۴ در یزد تا ۴۰ در تهران تغییر می‌کند).

آنچنان که جدول دوم نشان می‌دهد اگر همه داده‌ها را محسوب کنیم بجز انتخابات وین ۲۰۱۴ هیچیک با توزیع بینومیال سازگار نیستند. اما اگر نسبی بسنجیم برای وین ۲۰۱۵ و برلین این احتمال در ابعاد ۰.۰۰۰۱ تا ۰.۰۰۱ است در حالیکه برای ایران به استثنا اردبیل احتمال تصادفی بودن و همپوش بودن با توزیع بینومیال صفر است. حال چنانچه یکی دو زوج دور از انتظار و بی معنا را حذف کنیم مشاهده می‌کنیم که برای دو انتخابات وین و برلین احتمال تصادفی بودن به شدت افزایش می‌یابد اما هنوز برای لرستان، اصفهان و اردبیل و تا حدودی یزد احتمال تصادفی و همپوش بودن با توزیع بینومیال بسیار پائین است.

نتیجه این آزمون چنین است که نه تنها تعداد زیاد ضرایب ۱۰۰ (ٍE00) غیر عادی است بلکه در مجموع تکرار k صندوق‌های دیگر (Emnها با دیگر دو رقم‌های دست راست) نیز در سنجش با انتخابات سالم در وین و برلین از حالت عادی بدور است.

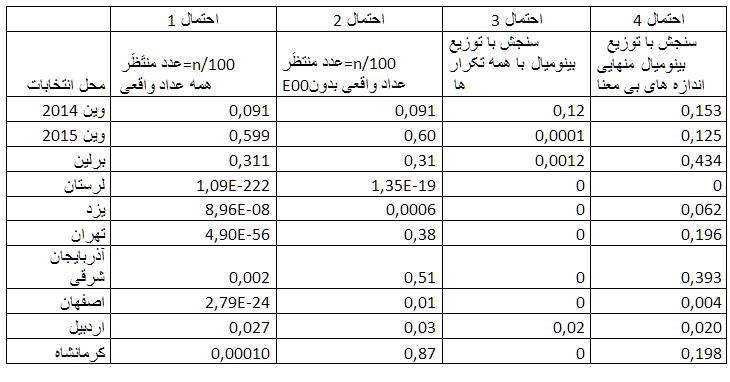
جدول ۲ : این جدول در بر گیرنده محاسبه احتمال۱ تا احتمال ۴ تصادفی یا تعمدی بودن بر مبنای آزمون chi square برای فراوانی تکرار دو رقم دست راست صندوق‌های رای است. ستون نخست از چپ نام محل انتخابات است. ستون دوم « احتمال ۱ » برای تعداد تکرار‌های معین از توزیع همشکلی Emn است در قیاس با اندازه منتظَر expected value که یکصدم تعداد کل صندوق‌های مربوطه است (N/۱۰۰). ستون سوم «احتمال ۲» یعنی تکرار ستون دوم پس از حذف E00، ستون جهارم «احتمال۳» آزمون chisq در قیاس با عدد منتظَر از توزیع بینومیال و در نظر گرفتن همه داده‌ها و ستون پنجم «احتمال ۴» تکرار ستون چهارم است پس از حذف E00‌ها و تعداد کمی از اندازه‌های واقعی برای همه مورد‌هائی که معنی دار نیستند و اثرشان بر نتیجه بسیار شدید است برای استان‌های ایران.

II. زمینه تئوریک کاربرد، توزیع بینومیال
با تقریبی نزدیک به یقین شمار همه آرای ماخوذه در صندوق‌ها در انتخابات نامبرده اعدادی سه و چهار رقمی هستند. احتمال اینکه دو رقم دست راست یعنی یکان و دهگان دو رقم معین مثلا ۰۰، ۵۹، ۰۵ و غیره... باشد یک صدم است. این ارقام را در نوشته حاضر با Emn خلاصه می‌کنم مثلا برای همه ضرایب ۱۰۰ که به ۰۰ ختم می‌شوند (یعنی m=۰ و n=۰) E00 یا E۵۹ (m=۵, n=۹)یا E۰۵ و...
فراوانی تکرار اعداد Emn در صندوق‌های رای از راه توزیع بینومیال binomial distribution بیان می‌شود. این توزیع آماری برای مواردی به گار برده می‌شود که:

۱. رخدادی مانند شمار آرای مأخوذ ه در یک صندوق به رخداد دیگر یعنی شمار آرا در دیگر صندوق بستگی نداشته باشد- مانند انداختن تاس در بازی تخت نرد که نتیجه نخستین پرتاب تاس اثری در پرتاب بعدی‌اش ندارد.

۲. احتمال رخدادهای ممکن ثابت باشد مثلا یک ششم ۶/۱برای هر تعداد چشمهای تاس از یک آزمون به آزمون دیگر. در مورد دو رقم نامبرده مجموع آرای ماخوذه به صندوق رای یکصدم ۱۰۰/۱ که برای همه صندوق‌ها یکسان و ثابت است.

۳. در هر آزمون بیش از دو امکان درست یا غلط (موفق یا ناموفق) موجود نباشد. مثلا تاس یا ۶ است (موفق) یا ۶ نیست (ناموفق) یا در مورد انتخابات مورد بحث، دو رقم E00 شمار آراء صندوق مثلا E00 است (موفق) یا E00 نیست (ناموفق)

۴. شمار آزمون‌ها معین باشد که در این مورد به معنی تعداد معین صندوق‌های رای است.

همه این چهار شرط نامبرده برای Emn معین از آرای ماخوذه صادق‌اند و از اینروی کار برد توزیع بینومیال برای توضیح توزیع دو رقم دست راست مجموعه آرا ی صندوق‌ها مجاز است.

با توجه به اینکه شمار آراء صندوق‌های مورد نظر ۳ یا چهار رقمی‌اند وقوع Emn معین آنها در شرایطی عاری از دستکاری، تصادفی است و با احتمال وقوع ۱۰۰/۱ (یکصدم) برای هر رخداد- مثلا احتمال اینکه E00 یا E45 یک یکبار رح دهند ۱۰۰/۱ (یکصدم) است.

فزون برین خروجی صندوق‌ها مستقل از یکدیگرند و رخدادن هر Emn دو امکان دارد مثبت یا منفی – یعنی مثلا تعداد کل آرای یک صندوق یا ضریبی است از ۱۰۰ یا چنین ضریبی نیست- و شمار دفعات آزمون هر بار معین است و این همان شمار صندوق‌های رای در هر محدوده جغرافیایی سیاسی است – مثلا در استان تهران.

آنچنان که در بالا اشاره شد اگر بخواهیم دریابیم که مثلا از هزار صندوق رای که هریک در بر گیرنده شماری از آراء حداقل سه رقمی باشند احتمال تکرار E00 چیست می‌توان از توزیع بینومیال استفاده کرد.

اگر تعداد آزمون‌ها برای رخداد X را n، احتمال یک رخداد را p، احتمال k بار تکرار این رخداد X را P(X=k) بنامیم فرمول توزیع بینومیال:

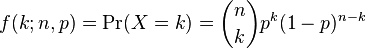
که در آن (k n) کمبیناسیون n آزمون است با k بار تکرار یک رخداد.

برای مثال اگر بخواهیم محاسبه کنیم که در تهران با n=۶۰۸۵ صندوق رای احتمال اینکه یک دو رقمی معین یکان و دهگان، مثلا E63، ۵۰ بار تکرار شود باید در فرمول بالا برای n ۶۰۸۵، برای k ۵۰ و برای p ۰.۰۱(یکصدم) بگذاریم و احتمال وقوع این رخداد را که P(E۶۳=۵۰) پیدا کنیم.

چنانچه احتمال P (X=k) را برای وقوع تکرار Emn در شمار آراء میان ۰، ۱،۲، ۳،... و هر اندازه دیگر را محاسبه کنیم به نقطه‌هایی دست خواهیم یافت که همه باهم (مکان هندسی شان) منحنی توزیع را نشان می‌دهند.

هر توزیع بینومیال دارای یک ماکزیمم است که اندازه مورد انتظار (expectation value) نامیده می‌شود و برابر است با حاصل ضرب شمار آزمون‌ها و احتمال وقوع یک رخداد. مثلا در تهران با شمار آزمون ۶۰۸۵ و احتمال ۰.۰۱ بیشترین تعداد وقوع دو رقم در تکرار k=۶۰ بار یا ۶۱ بار است. تکرار‌های بیشتر یا کمتر از این تعدادشان کوچکتر از این هستند.

کاربرد توزیع بینومیال در ارزیابی نتایج انتخابات خرداد ۱۳۸۸

برای آزمایش این تئوری نخست کوشش کردم آنرا در انتخاباتی که شبهه‌ای در سلامت شان نباشد بکار ببندم که همانا دو انتخابات شهر وین برای پارلمان اروپا ۲۰۱۴ و انتخابات ایالتی ۲۰۱۵ با حدود ۱۵۰۰ صندوق رای و انتخابات فدرال سال ۲۰۰۹ برلین با ۲۲۷۷ صندوق بوده‌اند.

این آزمون نشان می‌دهد که نتیجه عملی کسب شده در انتخابات با پیشبینی تئوریک توزیع بینومیال همخوانی دارد. نکته حائز اهمیت این است که در هیچیک از این سه انتخابات شمار تکرار Emn خارج از محدوده پیشبینی شده در تئوری وجود ندارد.

‌آزمودن فرض تئوریک در دو انتخابات وین و یک انتخابات از برلین به عنوان سه نمونه از انتخابات آزاد
آنگونه که در سه نمودار ۱، ۲ و ۳ زیرین برای انتخابات پارلمان اروپا در سال ۲۰۱۴، انتخابات مجلس ایالتی در وین و انتخابات فدرال ۲۰۰۹ برلین می‌توان مشاهده کرد توزیع بینومیال برای دو رقم پایانی Emn از ۱۵۴۳ صندوق رای، خارج از محدوده‌ای که تئوری پیشبینی می‌کند یعنی تکرار Emn کمتر از ۴-۵ و بیشتر از ۲۷-۲۸ بار رخ نداده است. این امر را می‌توان برای انتخابات سال ۲۰۱۵ وین نیز مشاهده کرد. شمار صندوق‌های رای در وین پیرامون ۱۵۰۰ بسیار نزدیک به کرمانشاه با بیش از۱۴۰۰ صندوق و لرستان با نزدیک به ۱۳۰۰ صندوق. در مورد انتخابات ۲۰۰۹ برلین نیز با شمار ۲۲۷۷ بسیار نزدیک به اصفهان با ۲۲۸۰ صندوق است.

هر سه انتخابات نشان می‌دهند که فراوانی تکرار‌های دو رقم یکان و دهگان معین Emn در محدوده پیشبینی شده تئوری اتفاق افتاده‌اند.

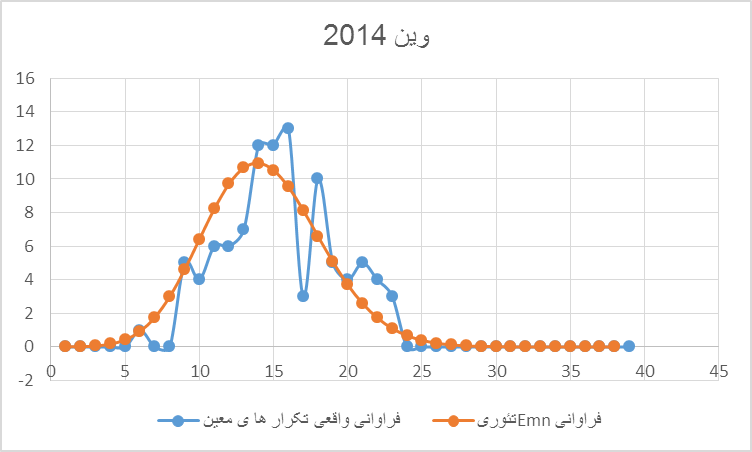
نمودار ۱:  احتمال وقوع تکرار Emn‌های معین واقعی و تئوری در انتخابات ۲۰۱۴ ایالت وین را نشان می‌دهد. محور افقی‌اش تعداد تکرار‌ها و محور عمودی فراوانی این تکرارهای را نشان می‌دهد. می‌توان مشاهده کرد که برای وین با حدود ۱۵۰۰ صندوق رای هیچ دو رقم آخری Emn شمار کل رای‌های ماخوذه‌ای وجود ندارد که فراتر از پیشبینی تئوریک یعنی ۵ بار تا ۲۵ بار تکرار شده باشد.. فزون برین بیشترین دفعات تکرار‌ها با بیشترین احتمال ۱ ٪ پیرامون ۱۵ بار Emn رخداده‌اند است- این را تعداد تکرار مورد انتظار می‌نامند expected value.

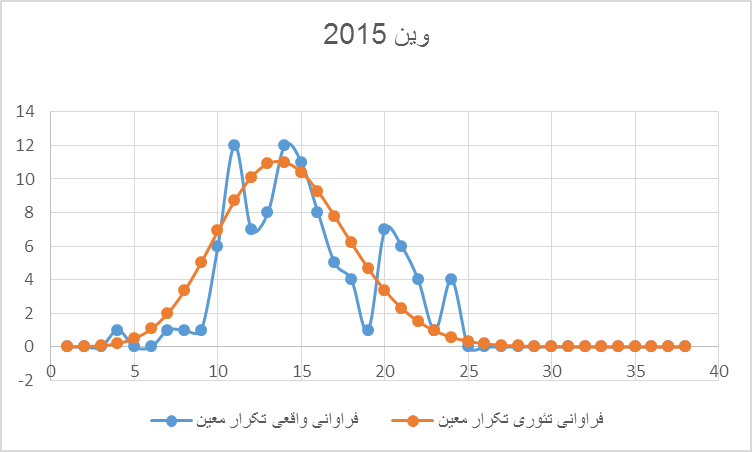
نمودار ۲: احتمال وقوع تکرار ٍEmn‌های معین واقعی (آبی) و تئوری (نارنجی) در انتخابات ۲۰۱۵ ایالت وین را نشان می‌دهد. محور افقی‌اش تعداد تکرار‌ها و محور عمودی فراوانی این تکرارهای را نشان می‌دهد. برای وین با حدود ۱۵۰۰ صندوق رای می‌توان مشاهده کرد که هیچ دو رقم آخری Emn شمار کل رای‌های ماخوذه‌ای وجود ندارد که فراتر از پیشبینی تئوریک یعنی ۴ بار تا ۲۵ بار تکرار شده باشد.. فزون برین بیشترین دفعات تکرار‌ها با بیشترین احتمال ۱ ٪ پیرامون ۱۵ بار Emn رخداده‌اند است- این را تعداد تکرار مورد انتظار می‌نامند

برلین انتخابات ایالتی ۲۰۰۹
برلین با نگاه به شمار ۲۲۷۷صندوق‌های رای گیری کاملا قابل سنجش با اصفهان (۲۲۸۰) است.

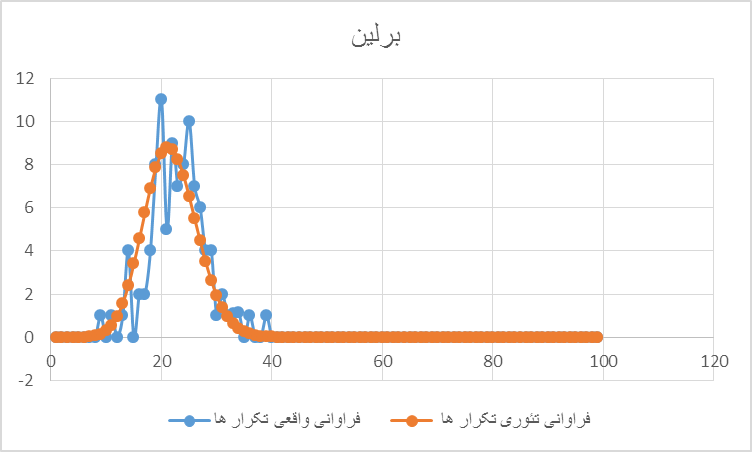
نمودار ۳: نتایج انتخابات ایالتی برلین در سال ۲۰۰۹. محور افقی تعداد تکرار‌های معین k و محوری عمودی فراوانی این تکرار‌ها را نشان می‌دهد. در خور توجه است که فراوانی تکرار Emn از محدوده قلمرو ۱۰-۴۰ پیشبینی شده به میانجی توزیع بینومیال فراتر نمی‌رود. نا محتمل ترین kها ۹ و ۳۹ با احتمالی رخداد شان برابر با ۰.۰۰۰۵ است. در سنجش با اصفهان می‌توان مشاهده کرد که برای k=۴۶, ۴۸, ۸۵ فراوانی بزرگتر از ۰ ظاهر نشده است.

انتخابات تهران
در انتحابات خرداد ۱۳۸۸ تهران دارای ۶۰۸۵ صندوق رای گیری بوده است. از این میان در ۲۱۶ صندوق E00 ظاهر شده‌اند در حالیکه احتمال رخدادن چنین واقعه‌ای کمتر از ۵۰-۱۰ یعنی عملا صفر است.

فزون براین نگاهی به نمودار توزیع تئوریک و واقعی در تهران نشان می‌دهد که بقیه نقاط واقعی نیز با آنچه که تئوری پیشبینی می‌کند همخوانی ندارند. فزون برین برای E00 با ۲۱۶ بار تکرار برای E50 با ۸۲ بار تکرار و E99 با ۷۹ بار تکرار نامحتمل‌اند.

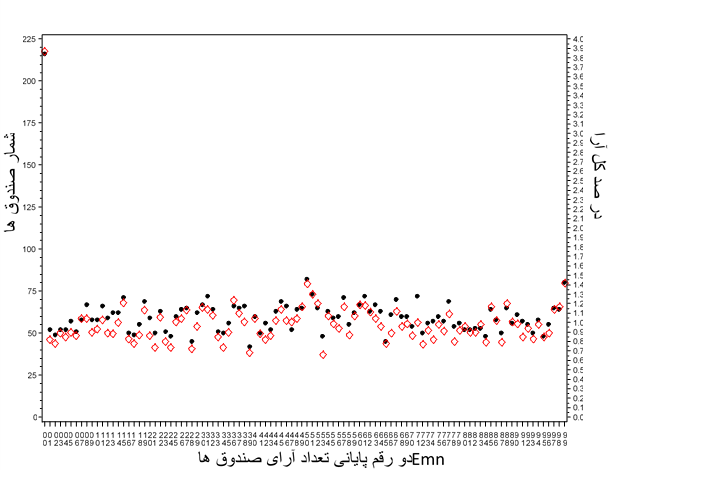
نمودار۴a: محور افقی صندوق‌ها با دو رقم پایانی مختلف از E00 تا...تا E۹۹ در اتنخابات خرداد ۱۳۸۸ تهران را نشان می‌دهد. محور عمودی دست چپ تعداد تکرار‌ها ی k دو رقم پایانی و محور عمودی دست راست سهم در صد ارای هر صندوق از کل آرای ماخوذه در تهران. نقطه‌های سیاه تعداد صندوق‌ها با یک Emn معین را و نقطه‌های مربع شکل در صد هریک از صندوق‌ها از کل آرای ماخوذه تهران را نشان می‌دهد. آشکارا می‌توان مشاهده کرد شمار صندوق‌ها منتهی به دو صفر E00 با ۲۱۶ بار،E۵۰ با ۸۲ بار تکرار و E۹۹ با ۷۹ بار تکرار و همچنین سهم در صدشان از مجموع آرای تهران برجسته‌اند. این نمودار را یکی از دوستان کارشناس آمار در اختیار م نهاده است

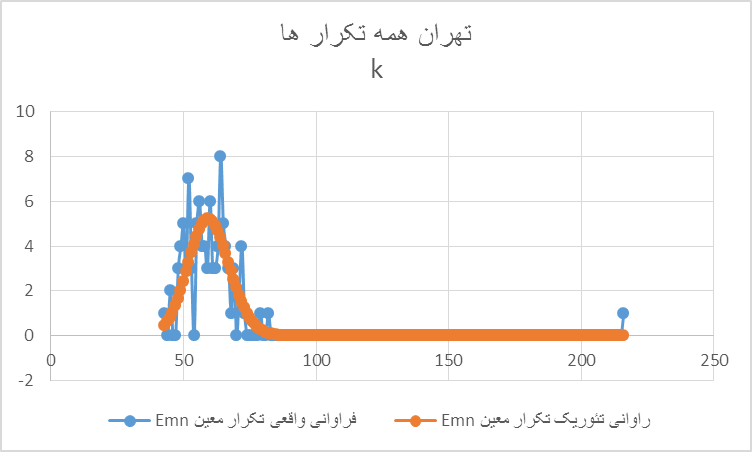
نمودار ۴b : توزیع Emn‌های مختلف برای انتخابات خردا ۱۳۸۸ در تهران. محور افقی تکرار‌ها k برای Emn‌ها و محور عمودی دفعاتی را که یک Emn معین برای یک تکرار معین ظاهر شده است ( مثلا تکرار E00 برای ۲۱۶ بار یکبار صورت گرفته است). از آنجا که احتمال تکرار ۲۱۶ باره بک Emn عملا صفر است، می‌توان نتیجه گرفت که چنین اتفاقی به طور تصادفی نمی‌تواند رخدهد بلکه نتیجه دستکاری هدفمند است. توزیع تئوریک احتمال وقوع یک Emn معین نشان می‌دهد که در تهران تکرار‌های یک Emn معین در محدوده ۴۰ تا ۸۰ محتمل است

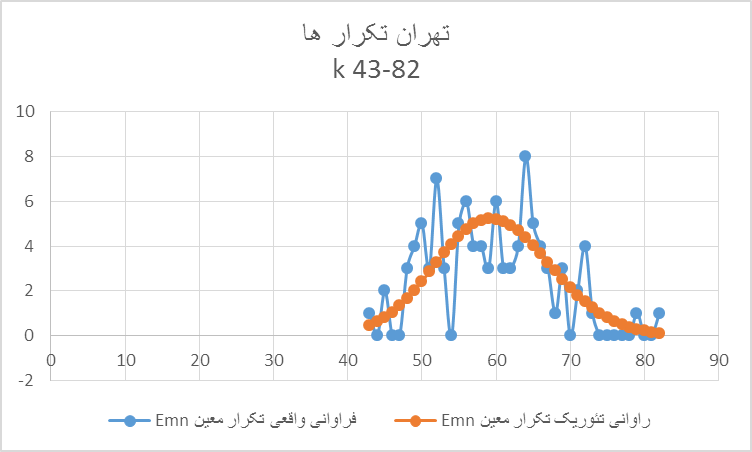
نمودار :۴c برای نشان دادن رفتار Emn در حیطه به لحاظ آماری محتمل (بدون E00 ) این نمودار تنها در بر گیرنده دامنه ۴۰ تا ۸۲ بار تکرار Emn‌های معین است. بروشنی می‌توان مشاهده کرد که تعدا تکرار‌ها دارای نوساناتی شدید است. مثلا نقطه ماکزیموم تئوری در k=۶۰ بکلی از نقاط ماکزیموم واقعی در تهران یعنی ۵۲ و ۶۵ بدورند.

انتخابات لرستان
استان لرستان دارای ۱۲۷۳ صندوق رای بوده است که از این میان ۱۳۲ بار E00 یعنی ۱۰.۳در صد با دو صفر پایانی، ۴۵ بار E50 و ۳۰ بار E97 و ۳۰ بار E99 که از این میان احتمال رخدادن شان به ترتیب ۱۰-۸۶، ۱۰-۱۳ و ۱۰-۵ است - دو احتمال اول عملا صفر و سومی برای وقوع، آن هم دوبار، بسیار نا محتمل. از اینروی آرای لرستان دلالت بر شدیدترین نوع دستکاری در نتایج آرا را در انتخابات خرداد ۱۳۸۸ به نمایش می‌گذارند.

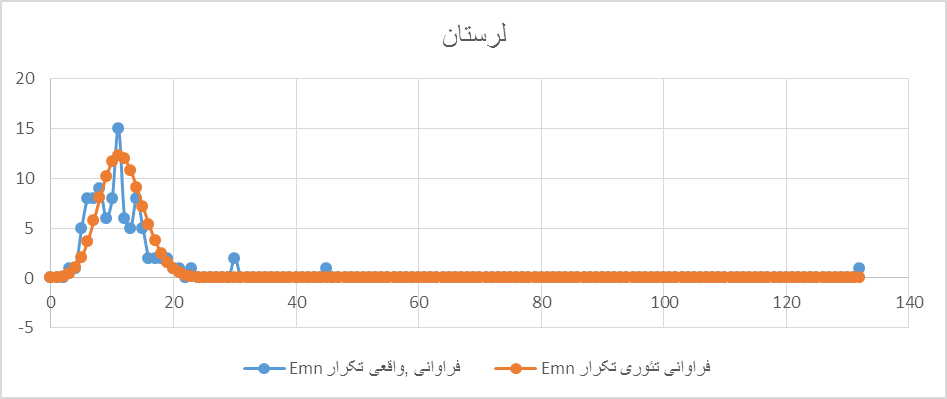
نمودار ۵a : محور افقی تعداد تکرار‌های Emn‌های معین را برای صندوق‌های رای لرستان نشان می‌دهد. می‌توان مشاهده کرد که تکرار ۱۳۲بار E00 و ۴۵ بار E۴۵ و ۳۰ بار E۹۷ و E۹۸ با احتمالی به ترتیب برابر با ۱۰-۸۶، ۱۰-۱۳ و ۱۰-۵ بسیار دور از انتظار تا غیر ممکن‌اند.

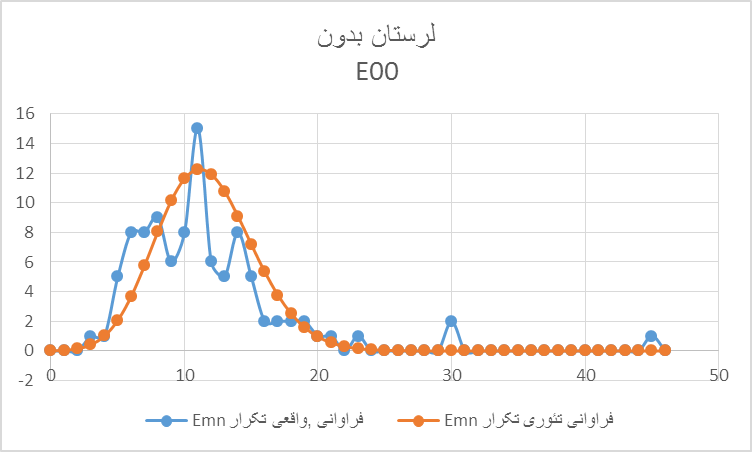
نمودار ۵b : محور افقی k یعنی تعداد تکرار‌های Emn‌های معین را برای صندوق‌های رای لرستان و محور عمودی فراوانی رخ دادن Emn‌های مختلف را بدون E00=۲۱۶ نشان می‌دهد( E00=۲۱۶ برای بهتر نشاندادن دیگر داده‌ها از گستره این نمودار خارج شده است). این نمودار پیشبینی تئوریک (نارنجی) را نشان می‌دهد که در انطباق با توزیع بینومیال فراوانی تکرار‌های محتمل میان ۳ تا ۲۳ دارای احتمالی عملا بزرگتر از صفر‌اند و خارج از این محدوده احتمالاتی عملا صفر.

استان یزد
استان یزد دارای ۶۹۲ صندوق اخذ رای بوده است که از این میان کل شمار ارای۲۵ صندوق از آن‌ها ضریبی از ۱۰۰ یعنی E00 ۲۵ بار تکرار شده است که برابر است با ۳.۶٪. احتمال بروز چنین رخدادی ۵,۱۳E-۰۸ یا پنج صدمیلیونم است. ۱۶ بار نیز E۵۰ تکرار شده است با احتمالی برابر با ۰,۰۰۱۲. جالب اینجا است که در بخش مرکزی شهر یزد با ۲۰۷ صندوق ۷.۲٪ صندوق‌ها E00 هستند. اینکه در مراکز کلان شهرها مانند یزد سهم صندوق‌های E00 بیش از دهات و شهر‌های خاشیه‌ای و دور افتاده است ناقض این ادعا است که گویا وجود بیش از انتظار E00‌ها پیامد کمبود برگ‌های تعرقه‌های رای بوده است.

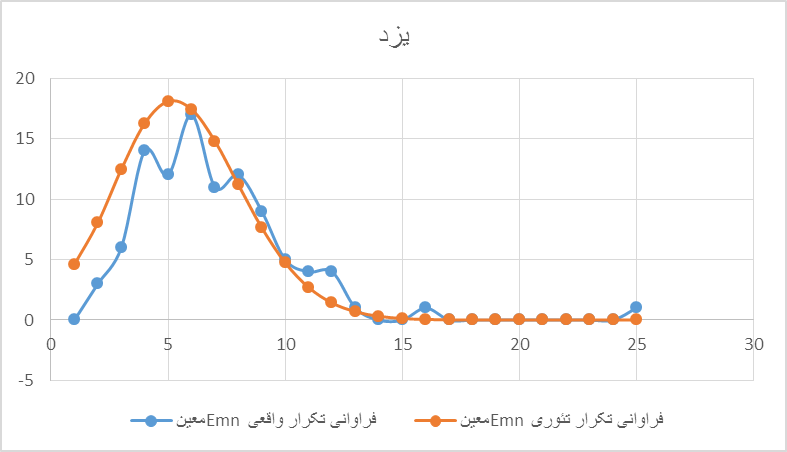
نمودار ۶: توزیع فراوانی واقعی (آبی) و تئوری(نارنجی) یک Emn معین در استان یزد. در این نمودار می‌توان و جود صندوق‌هائی را مشاهده کرد مانند ۲۵ بار و ۱۶ بار تکرار یک Emn معین که کاملا خارج از گستره پیشبینی شده تئوریک هستند با احتمالی به ترتیب ۵,۱۳-۰۸ یا پنج صدمیلیونم و ۰,۰۰۱۲ در قیاس با ۰.۰۱ احتمال مورد انتظار.

استان آذربایجان شرقی
از ۲۷۶۵ صندوق رای ۶۴ بار E00 وجود داشته‌اند (۶۴ صندوق با ارقام پایانی ۰۰ یعنی E00 که احتمال رخدادنش ۱*۱۰-۹ - یک میلیاردیم- است، وجود داشته اند). ارقام این استان نشان می‌دهند که در قیاس با دیگر استان‌های مورد مطالعه، دستکاری در آنجا نظر به ملاحظات قومی با احتیاط بیشتر صورت گرفته است.

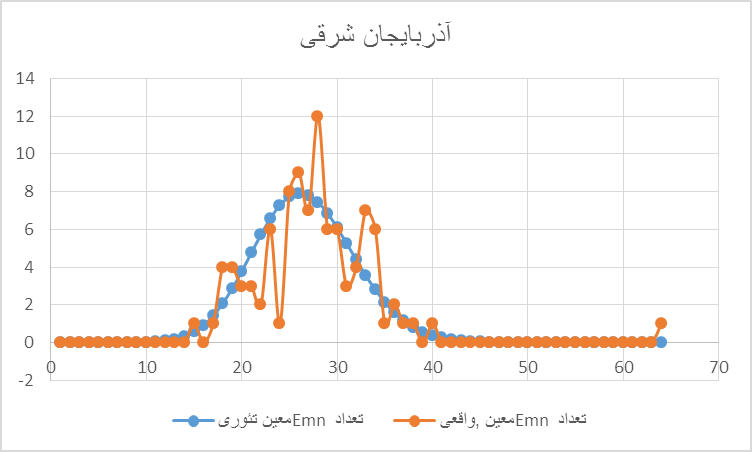
نمودار ۷ : محور افقی تعداد تکرار‌های Emn‌های معین را برای صندوق‌های رای آذربایجان شرقی و محور عمودی فراوانی رخ دادن Emn‌های مختلف را نشان می‌دهد. می‌توان مشاهده کرد که تکرار ۶۴بار ه E00 با احتمال یک میلیاردیم بسیار دور از انتظار تا غیر ممکن است همچنین می‌توان مشاهده کرد که فارغ از E00 دیگر نقاط نیز تا چه اندازه پراکنده و بی سامانمند‌اند.

استان اصفهان:
استان اصفهان دارای ۲۲۸۸ صندوق اخذ رای بوده است که از میان آنها محتوای ۸۷ صندوق ضریبی از ۱۰۰ بوده است، یعنی ۸۷ بار E00 تکرار شده است (۳.۸۲٪ کل صندوق‌ها). فزون برین۸۷ تکرار ۴۸ بار E۵۰ و ۴۶ بار E۹۹ نیز تکرار شده‌اند که احتمال وقوع شان به ترتیب ۳*۱۰-۲۵، شش میلیونیم و ۱.۳ میلیونیم در برابر ۰.۰۱ احتمال مورد انتظار است. فزون برین از ۵۳۲ صندوق مرکزی شهر اصفهان ۳.۹۵٪ ضریب ۱۰۰ یعنی E00 بوده‌اند. در اینجا هم می‌بینیم که توضیح فزونی E00‌ها از راه کمبود تعرفه‌های رای در حاشیه‌های دور افتاده دچار تناقض می‌شود.

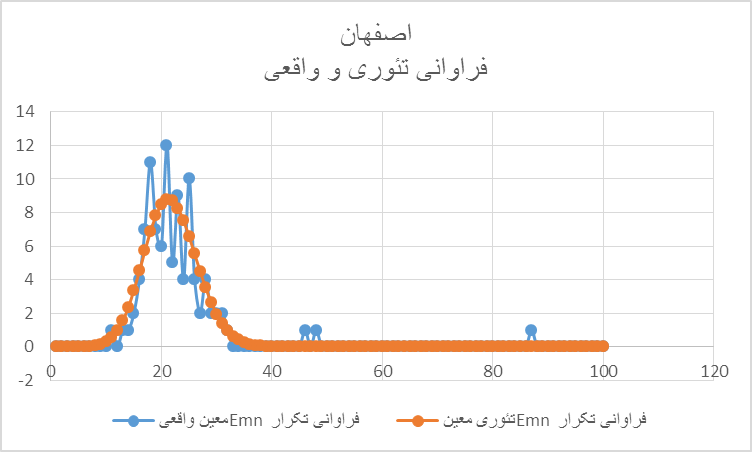
نمودار ۸: توزیع فراوانی تکرار Emn‌های معین واقعی و تئوری برای استان اصفهان. تکرار‌های ۸۷، ۴۸، و ۴۶ باره خارج از گستره پیشبینی شده از جانب تئوری هستند با احتمالاتی بسیار کم - به ترتیب ۳*۱۰۲۵، ۶*۱۰-۶ و ۱.۳ میلیونیم در برابر ۰.۰۱ احتمال مورد انتظار -. در درون حیطه پیشبینی شده نیز تغییرات داده‌ها نسبت به تئوری بسیار شدید است ( لطفآ این نمودار را با نمودار ۳ مربوط به برلین مقایسه کنید.

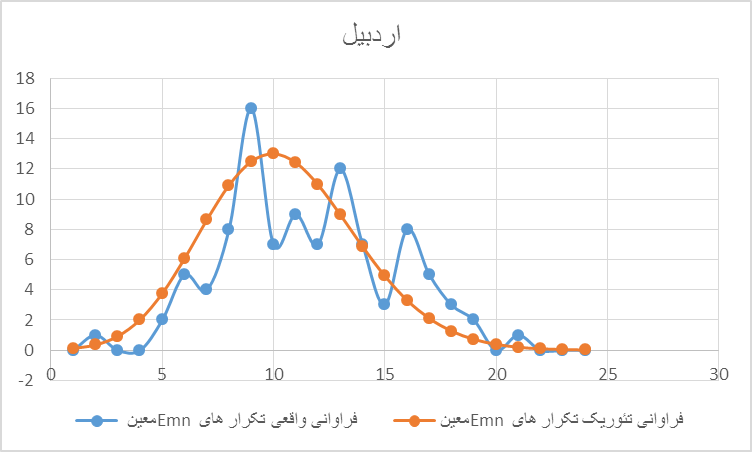
استان اردبیل: این استان دارای ۱۱۵۶ صندوق رای گیری بوده است. از این میان تعداد تکرار‌ها تا حدودی در چهارچوب مورد انتظار بوده‌اند. همه تکرار‌ها در گستره تئوریک میان ۱ بار تا بیست بار هستند با اندک تفاوتی برای E00 که با ۲۲ بار تکرار احتمالی در حدود ۰.۰۰۱ دارد. اختلاف در در صد بروز E00 در شهر اردبیل و کل استان چندان بزرگ نیست ( ۱.۲۳٪ در برابر ۱.۹۱٪ به ترتیب)

استان کرمانشاه
استان کرمانشاه دارای ۱۴۳۵ صندوق رای بوده که از میان آن‌ها ۴۷ صندوق E00 بوده‌اند. احتمال رخدادن چنین تکراری ۳*۱۰-۱۲ و بدینگونه نزدیک به صفر است.

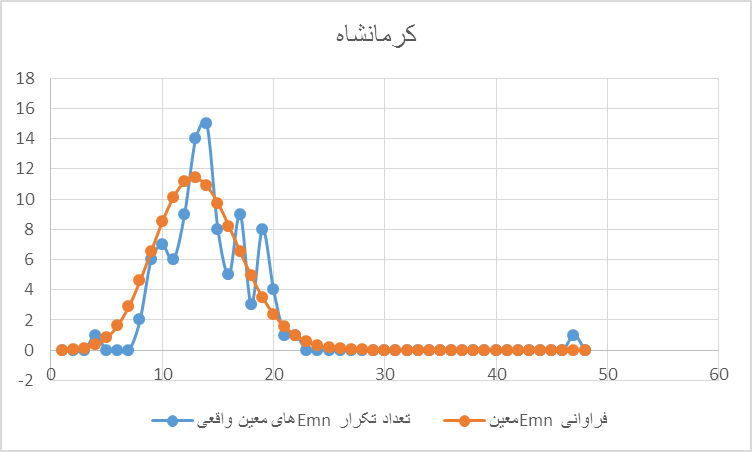
نمودار ۹: محور افقی تعداد k تکرار‌های Emn‌های معین را برای صندوق‌های رای کرمانشاه و محور عمودی فراوانی رخ دادن Emn‌های مختلف را نشان می‌دهد. می‌توان مشاهده کرد که تکرار ۴۷ بار ه E00 با احتمال ۴*۱۰-۱۲چهار تریلیاردیم بسیار دور از انتظار تا غیر ممکن است.

سنجش تصادفی بودن کل Emn‌ها
مقدمتا در خور توجه است که چه در انتخابات سالم مانند وین و برلین و چه در انتخاباتی که ظن دستکاری و عدد سازی در آن‌ها وجود داشته باشد، مانند انتخابات ۱۳۸۸ ایران (مندرج در جدول ۲)، همه داده‌ها به درجات معینی تصادفی‌اند. یعنی حتی اگر اعداد ساختگی هم باشند باز روند ساختن شان تا حدودی تصادفی است با این قید که نتیجه تجمیع آن‌ها باید با نتیجه از پیش تعیین شده‌ای همپوش باشد. از اینروی قضاوت دقیق در پاره‌ای از موارد مشکل است. از اینروی هدف از این آزمون تکمیل نکات مندرج در در جدول ۱ است که خود به اندازه کافی گویا هستند. می‌خواهیم بیازماییم که آیا می‌توان گرایشی به سوی واقعی یا دستکاری بودن را شناسائی کرد.

برای آزمون این فرضیه که ارقام تکرار Emn نتیجه رخداد‌های تصادفی هستند یا نتیجه عوامل دیگر، در آمار روشی متداول است که »آزمون توان دوم شی» Chi-square Test نام دارد. در این آزمون داده‌های واقعی رخداده با انداره‌ای که انتظار می‌رود داشته باشند یعنی اندازه‌های منتظَر expected value سنجیده می‌شوند و احتمال پذیرش یا رد فرضیه درستی و تصادفی بودن اعداد محاسبه می‌شود.

این آزمون دارای یک فرضیه صفر H۰= null hypothesis است دایر بر اینکه نتایج (ارقام) کسب شده (واقعی) اختلاف معنا داری با نتایج (ارقام) مورد انتظار (منتظَر) ندارند. آنگاه یک احتمال تعریف می‌شود بدینگونه که اگر احتمال صحت این فرضیه بیشتر از این احتمال تعریف شده باشد در آن صورت فرضیه ۰ معنا ندارد یا به عبارت دیگر نتایج کسب شده با آنچه انتظار می‌رفت اختلاف معنا داری ندارد و تصادفی‌اند (فارغ از دستکاری). برای انجام این محاسبات باید اندازه chi square محاسبه و احتمال مربوطه برای تصمیم گیری از جدول‌های ویژه این کار استخراج شوند. در مطالعات آماری متداول است که این احتمال مرجع ۰.۰۵ (۵٪) است.

آزمون chi square را به دو شیوه انجام داده‌ام:
الف: آزمون همشکلی uniformity :‌ شمار تکرار k همه دو رقم‌های سمت راست ( Emn‌ها ) در قیاس با عدد n/۱۰۰ که در آن n تعداد کل صندوق‌های هر استان معین است.

ب: همپوشی با توزیع بینومیال binomial fit :فراوانی واقعی تکرار‌های Emn‌های معین در قیاس با اندازه منتظَری که از توزیع بینومیال binomial distribution استخراج می‌شود.

این آزمون برای وین، برلین، لرستان، تهران، آذربایجان شرقی، یزد، اصفهان، اردبیل و کرمانشاه انجام گرفته نتایج‌اش در جدول ۲ مندرج است.

نتیجه گیری:
نشانه‌های بارزی وجود دارد که تعداد آرای ریخته شده به صندوق‌ها اعداد تصادفی آنچنان که از یک انتخابات سالم انتظار می‌رود، نیستند. این واقعیت هر چند که در تعداد کل آرا که ضریبی از ۱۰۰ هستند تجلی‌ای ویژه می‌ایند اما منحصر به آن‌ها نیستند. رفتار دیگر شمار کل رای‌های صندوق‌ها که صریبی از ۱۰۰ نیستند هم خارج از انتظار است. به عبارت دیگر تقلب تنها در وجود ضریب‌های ۱۰۰ خلاصه نمی‌شود بلکه در تقسیم عامدانه همه ارقام. ضریب ۱۰۰‌ها تنها سرنخ دستکاری هدفمند را آشکار می‌کنند.

به احتمال قریب به یقین در نتایج انتخابات خرداد ۱۳۸۸ ریاست جمهوری ایران تقلب در حد عدد سازی صورت گرفته است. در لرستان بیشترین اندازه عدد سازی عریان صورت گرفته است. به نظر می‌اید که در مجموع، آرا صندوق‌ها به نحوی در میان کاندیدا‌ها تقسیم شده‌اند که به نتیجه از پیش اعلام شده برسند.

بهروز بیات
اردیبهشت۱۳۹۶

این پژوهش در خرداد ۹۵ در وبسایت زیتون انتشار یافت و اکنون با اندکی تغییر و ویرایش نظر به امکان مطرح و حاد شدن مجدد تقلب در انتخابات ۹۶ انتشار می‌یابد.